Sieving chatGPT

Sun, Dec 11, 2022

I had my first chat with chatGPT, the latest large language model sensation. It is amusing, very chatty, and in many ways impressive. But it is often a little (or very) wrong and misses the subtleties. This happened in many topics, with more gross errors in more specialized topics. I have gathered here one thread of conversation on something these models generally do well.

Much of my conversation was about getting chatGPT to program the Sieve of Eratosthenes in Python. It is very convincing and gives clear explanations, but with mistakes in the code. It took some back and forth for it to get a “correct” implementation, in the sense that it ran and gave the correct answer.

But even this missed the main point of the sieve algorithm, which makes it efficient. The code of chatGPT effectively checked divisibility by computing remainders for all pairs – essentially the brute force way. As a result it took over 12 seconds to compute primes to a million, while my modification to get a genuine sieve found such primes in under 0.05 seconds and the primes up to 10 million in less than half a second.

The bulk of this post is our conversation about the sieve. In the afterword I discuss the problems with its final algorithm and give the improved one. But before that, I give an example of language models in action in some of my work with collaborators.

Autoformalization

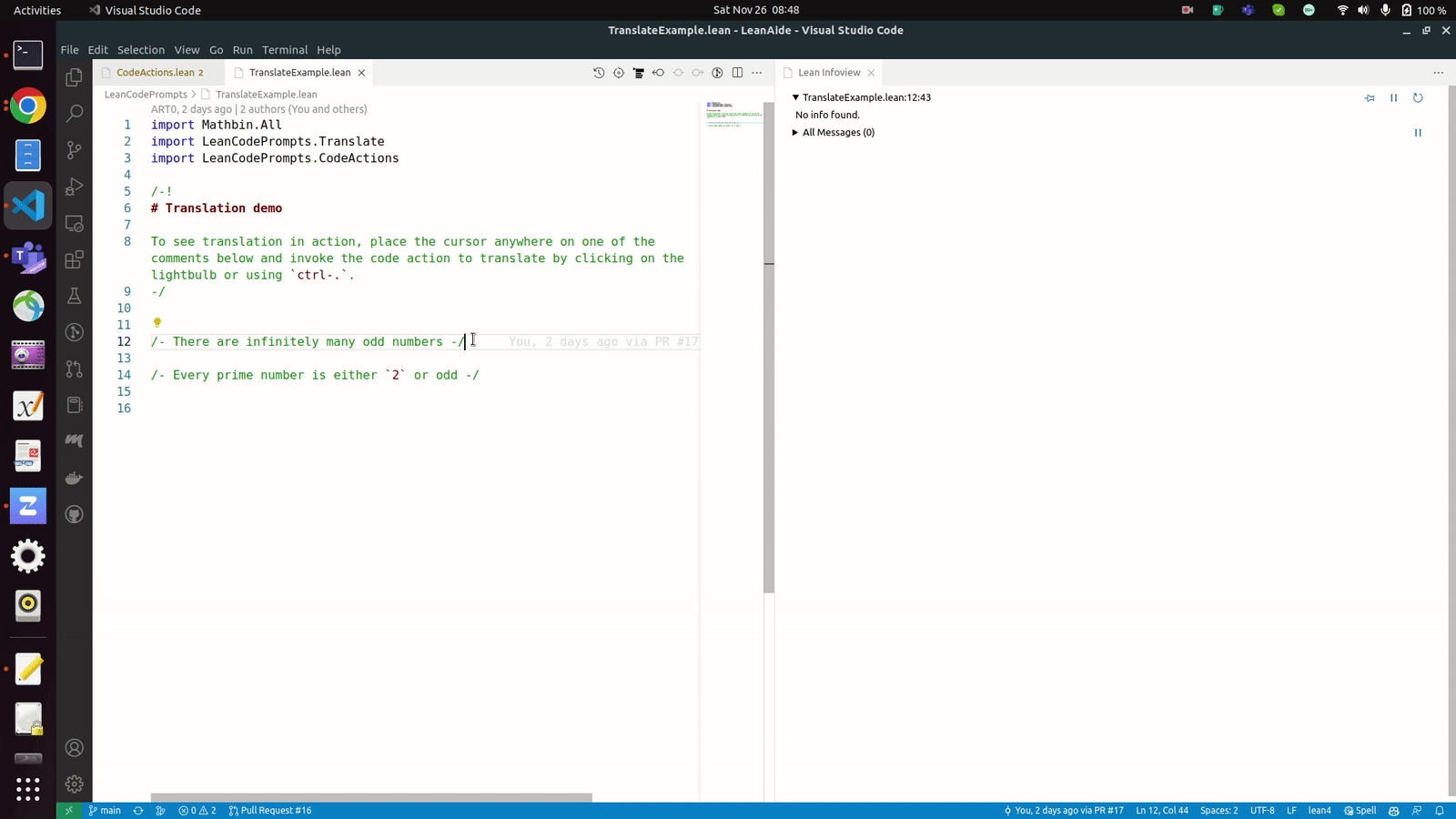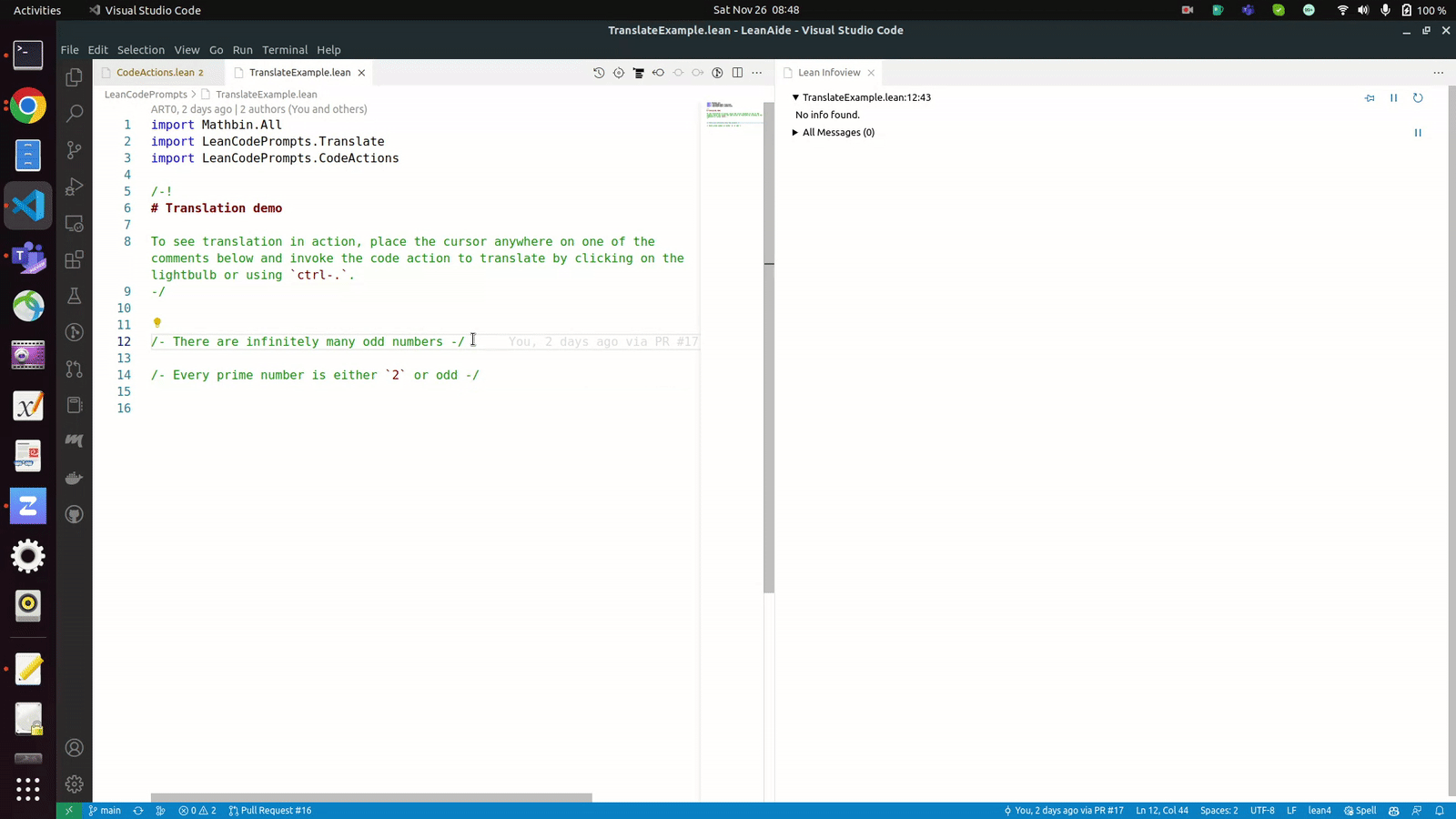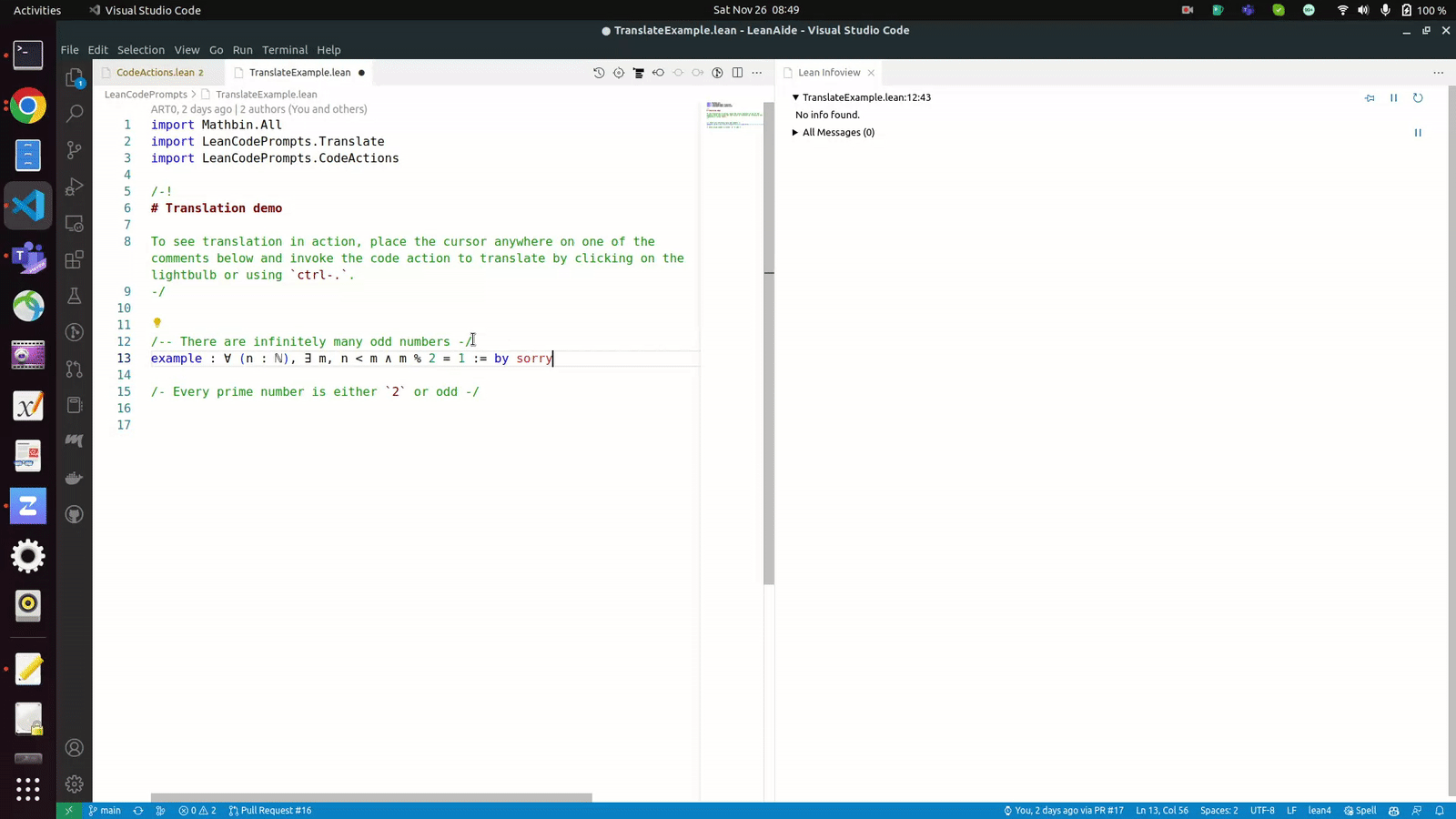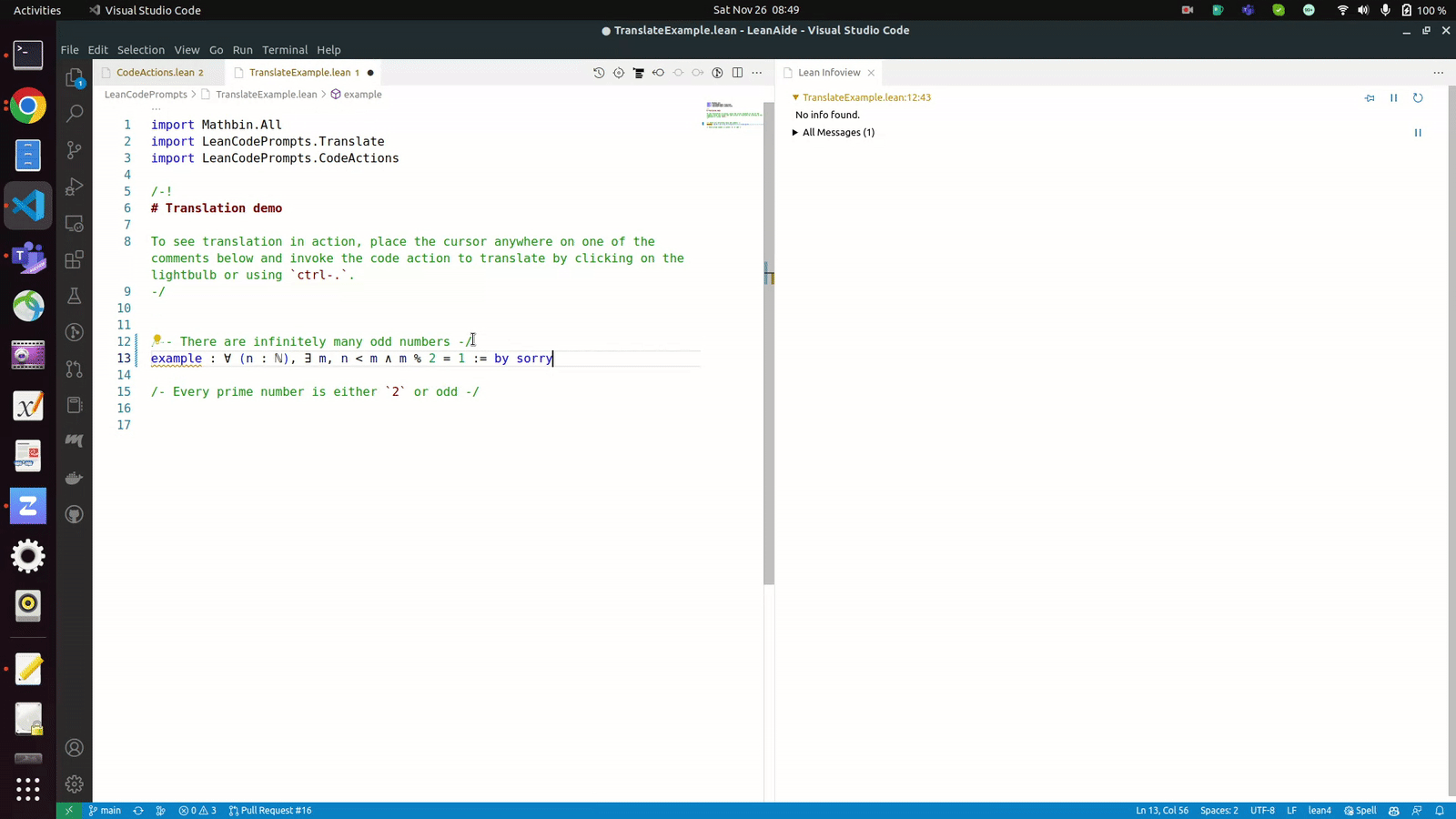
We have been working on a tool, using a large language model (Codex), for AI based translation from natural language to Lean 4 with a convenient interface.

A quick demo of this in action:
A brief video: https://youtu.be/_NMquXd0Qos

The code is at https://github.com/siddhartha-gadgil/LeanAide with details and instructions for trying it out in the README. The Lean code was written by Anand Rao and myself, and is part of a collaboration with Ayush Agrawal, Ashvni Narayanan, and Navin Goyal.

The Conversation

We come now to the conversation with chatGPT. My questions begin with [Siddhartha] and are quoted.

[Siddhartha] How does one implement Eratosthenes sieve in python?

The Sieve of Eratosthenes is an algorithm for finding all prime numbers up to a given integer n. The algorithm works by iterating over all integers from 2 to n, and marking each integer that is not prime as composite. This is done by starting with the smallest prime number (2), and then marking all its multiples as composite. The process is repeated for the next smallest prime number, and so on, until all numbers up to n have been either marked as prime or composite. The numbers that remain unmarked at the end of the process are the prime numbers between 2 and n.

To implement the Sieve of Eratosthenes in Python, we can follow these steps:

Define a list of integers from 2 to n, which will be used to store the prime and composite numbers.
Define a boolean variable is_prime initialized to True, which will be used to mark each number as either prime or composite.
Iterate over the list of integers from 2 to n, and for each integer i:
1. Set the value of is_prime to True.
2. Iterate over the list of integers from 2 to n, and for each integer j such that j is not equal to i and j is a multiple of i:
  1. Set the value of is_prime to False.
3. If the value of is_prime is True, append i to the list of prime numbers.
Return the list of prime numbers.

This is a simple and efficient implementation of the Sieve of Eratosthenes in Python, and it can be used to find all prime numbers up to a given integer n. To further optimize the algorithm, we can use additional data structures and techniques, such as a bit array or a segmented sieve, to reduce the memory and time complexity of the algorithm.

[Siddhartha] Can you give the code?

Yes, here is a simple implementation of the Sieve of Eratosthenes in Python that uses a list of integers to store the prime and composite numbers, and a boolean variable to mark each number as either prime or composite:

def sieve_of_eratosthenes(n):
    # Define a list of integers from 2 to n
    numbers = [i for i in range(2, n+1)]

    # Define a boolean variable to mark each number as either prime or composite
    is_prime = True

    # Iterate over the list of numbers
    for i in numbers:
        # Set the value of is_prime to True
        is_prime = True

        # Iterate over the list of numbers
        for j in numbers:
            # If j is not equal to i and j is a multiple of i, set the value of is_prime to False
            if j != i and j % i == 0:
                is_prime = False

        # If the value of is_prime is True, append i to the list of prime numbers
        if is_prime:
            prime_numbers.append(i)

    # Return the list of prime numbers
    return prime_numbers

# Test the sieve_of_eratosthenes function
print(sieve_of_eratosthenes(10)) # [2, 3, 5, 7]
print(sieve_of_eratosthenes(20)) # [2, 3, 5, 7, 11, 13, 17, 19]

This implementation of the Sieve of Eratosthenes in Python is simple and easy to understand, and it can be used to find all prime numbers up to a given integer n. The function takes a single argument n, which is the upper bound of the range of numbers to be searched for prime numbers, and it returns a list of prime numbers between 2 and n. The function uses two for loops to iterate over the list of numbers, and a conditional statement to mark each number as either prime or composite. The function can be further optimized and improved by using additional data structures and techniques, such as a bit array or a segmented sieve, to reduce the memory and time complexity of the algorithm.

[Siddhartha] The variable is_prime should be a list, and updated for the specific number

Yes, you are correct. The variable is_prime should be a list of boolean values, and it should be updated for each number in the list of numbers. The variable is_prime is currently a single boolean variable, and it is overwritten in each iteration of the outer for loop, which means that it does not store the prime and composite status of each number in the list of numbers.

To fix this issue, we can replace the variable is_prime with a list of boolean values, where each value in the list corresponds to a number in the list of numbers, and indicates whether the number is prime or composite. Then, we can update the value of each element in the list of boolean values using a nested for loop, instead of using a single boolean variable. This will ensure that the list of boolean values stores the prime and composite status of each number in the list of numbers, and that the function returns the correct list of prime numbers.

Here is an updated implementation of the Sieve of Eratosthenes in Python that uses a list of integers to store the prime and composite numbers, and a list of boolean values to mark each number as either prime or composite:

def sieve_of_eratosthenes(n):
    # Define a list of integers from 2 to n
    numbers = [i for i in range(2, n+1)]

    # Define a list of boolean values to mark each number as either prime or composite
    is_prime = [True for i in range(2, n+1)]

    # Define a list of prime numbers
    prime_numbers = []

    # Iterate over the list of numbers
    for i in range(2, n+1):
        # Set the value of is_prime[i] to True
        is_prime[i] = True

        # Iterate over the list of numbers
        for j in range(2, n+1):
            # If j is not equal to i and j is a multiple of i, set the value of is_prime[j] to False
            if j != i and j % i == 0:
                is_prime[j] = False

        # If the value of is_prime[i] is True, append i to the list of prime numbers
        if is_prime[i]:
            prime_numbers.append(i)

    # Return the list of prime numbers

[Siddhartha] It is unnecessary to set the individual variable as True. Instead you should check if it is True and skip the loop if it is false.

You are correct. In the updated implementation of the Sieve of Eratosthenes in Python, it is unnecessary to set the value of the element is_prime[i] to True in each iteration of the outer for loop. Instead, we can check if the value of is_prime[i] is True, and skip the inner for loop if it is not True. This will reduce the time complexity of the algorithm by avoiding unnecessary computations, and it will make the implementation more efficient and elegant.

def sieve_of_eratosthenes(n):
    # Define a list of integers from 2 to n
    numbers = [i for i in range(2, n+1)]

    # Define a list of boolean values to mark each number as either prime or composite
    is_prime = [True for i in range(2, n+1)]

    # Define a list of prime numbers
    prime_numbers = []

    # Iterate over the list of numbers
    for i in range(2, n+1):
        # If the value of is_prime[i] is False, skip the inner for loop
        if not is_prime[i]:
            continue

        # Iterate over the list of numbers
        for j in range(2, n+1):
            # If j is not equal to i and j is a multiple of i, set the value of is_prime[j] to False
            if j != i and j % i == 0:
                is_prime[j] = False

        # If the value of is_prime[i] is True, append i to the list of prime numbers
        if is_prime[i]:
            prime_numbers.append(i)

    # Return the list of prime numbers
    return prime_numbers

# Test the sieve_of_eratosthenes function
print(sieve_of_eratosthenes(10)) # [2, 3, 5, 7]
print(sieve_of_eratosthenes(20)) # [2, 3, 5, 7, 11, 13, 17, 19]

In this updated implementation of the Sieve of Eratosthenes in Python, we added a continue statement in the outer for loop to skip the inner for loop if the value of is_prime[i] is not True. This will avoid unnecessary computations and reduce the time complexity of the algorithm. The function can be further optimized and improved by using additional data structures and techniques, such as a bit array or a segmented sieve, to reduce the memory and time complexity of the algorithm.

[Siddhartha] When I run the python code, I get ‘‘IndexError: list assignment index out of range" on line 21

Yes, you are correct. The previous implementation of the Sieve of Eratosthenes in Python is incorrect, as it attempts to assign a value to an element of the is_prime list at an index that is out of range, resulting in the IndexError that you have encountered. The is_prime list is initialized with True values for all indices from 2 to n, but the inner for loop attempts to update the value of is_prime[j] for all indices j that are multiples of i, where i is an index in the range from 2 to n. This means that the index j may be greater than n, which is out of range for the is_prime list, resulting in the IndexError.

To fix this error, we need to modify the inner for loop to only update the value of is_prime[j] for indices j that are in the range from 2 to n, by using the range function to generate a list of indices from 2 to n and the enumerate function to iterate over the list of indices and their corresponding values. Here is a corrected implementation of the Sieve of Eratosthenes in Python that uses the range and enumerate functions to iterate over the list of indices and update the is_prime list only for indices in the range from 2 to n:

def sieve_of_eratosthenes(n):
  # Define a list of integers from 2 to n
  numbers = list(range(2, n+1))

  # Define a list of boolean values to mark each number as either prime or composite
  is_prime = [True] * (n+1)

  # Define a list of prime numbers
  prime_numbers = []

  # Iterate over the list of numbers
  for i, number in enumerate(numbers):
    # If the value of is_prime[i] is False, skip the inner for loop
    if not is_prime[i]: continue

    # Iterate over the list of numbers
    for j, candidate in enumerate(numbers):
      # If j is not equal to i and j is a multiple of i, set the value of is_prime[j] to False
      if j != i and candidate % number == 0: is_prime[j] = False

    # If the value of is_prime[i] is True, append number to the list of prime numbers
    if is_prime[i]: prime_numbers.append(number)

  # Return

[Siddhartha] I think the code is incomplete

Yes, you are correct. The previous implementation of the Sieve of Eratosthenes in Python is incomplete, as it is missing the final return statement that returns the list of prime numbers. Here is a complete implementation of the Sieve of Eratosthenes in Python that uses the range and enumerate functions to iterate over the list of numbers and update the is_prime list only for indices in the range from 2 to n:

def sieve_of_eratosthenes(n):
  # Define a list of integers from 2 to n
  numbers = list(range(2, n+1))

  # Define a list of boolean values to mark each number as either prime or composite
  is_prime = [True] * (n+1)

  # Define a list of prime numbers
  prime_numbers = []

  # Iterate over the list of numbers
  for i, number in enumerate(numbers):
    # If the value of is_prime[i] is False, skip the inner for loop
    if not is_prime[i]: continue

    # Iterate over the list of numbers
    for j, candidate in enumerate(numbers):
      # If j is not equal to i and j is a multiple of i, set the value of is_prime[j] to False
      if j != i and candidate % number == 0: is_prime[j] = False

    # If the value of is_prime[i] is True, append number to the list of prime numbers
    if is_prime[i]: prime_numbers.append(number)

  # Return the list of prime numbers
  return prime_numbers

# Test the sieve_of_eratosthenes function
print(sieve_of_eratosthenes(10)) # [2, 3, 5, 7]
print(sieve_of_eratosthenes(100)) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]

[Siddhartha] Thanks. The code is now correct

You’re welcome! I’m glad that the revised implementation of the Sieve of Eratosthenes in Python is working correctly for you. Let me know if you have any other questions.

Afterword

I accepted the code once it ran. But looking at the code, it is clear that it misses the main point of the sieve of Eratosthenes. Once a number $i$ is found to be a prime, in the sieve we run through multiples of this that are less than $n$, which are just numbers of the form $i * j$ for $2\leq j\leq n/i$. These are marked to be composite. No further check is needed for divisibility by $i$ – these are exactly the numbers between $2$ and $n$ that are divisible by $i$ other than $i$. The code of chatGPT does not do this. It checks divisibility by $i$ for all numbers between $2$ and $n$, making it essentially a brute force primality check for each number instead of a sieve. In fact chatGPT makes comments about improving using low-level optimizations while missing the main conceptual optimization of the sieve of Eratosthenes.

Below is the improved code along the lines of the above (I have also simplified looping due to my own lack of experience with enumerate, and avoided the continue by nesting within an if). The code of chatGPT took over 12 seconds to find primes up to a million while the below code found these in under 0.05 seconds and found primes up to 10 million in less than half a second.

def sieve_of_eratosthenes(n):
  # Define a list of integers from 2 to n
  numbers = list(range(2, n+1))

  # Define a list of boolean values to mark each number as either prime or composite
  is_prime = [True] * (n+1)

  # Define a list of prime numbers
  prime_numbers = []

  # Iterate over the list of numbers
  for i in range(2, n+ 1):
    # If the value of is_prime[i] is False, skip the inner for loop
    if is_prime[i]: 
        # Iterate over the list of numbers
        for j in range(2, (n //i) + 1):
        # set the value of is_prime[i * j] to False
           is_prime[i * j] = False
        # append i to the list of prime numbers
        prime_numbers.append(i)

  # Return the list of prime numbers
  return prime_numbers

# Test the sieve_of_eratosthenes function
print(sieve_of_eratosthenes(10)) # [2, 3, 5, 7]
print(sieve_of_eratosthenes(100)) # [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
print(sieve_of_eratosthenes(1000000))